How to Know if a Transformationis Telling You to Reflect the X or Y Axis
Function Reflections
The terminal two like shooting fish in a barrel transformations involve flipping functions upside down (flipping them around the x -axis), and mirroring them in the y -axis.
The first, flipping upside downwardly, is institute past taking the negative of the original role; that is, the dominion for this transformation is –f(x).
To run across how this works, take a look at the graph of h(x) = x 2 + iix – three. The graph of the original function looks similar this:
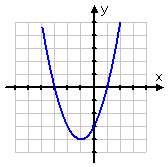
Content Continues Beneath
To imagine this graph flipping upside-downwardly, imagine that the graph is drawn on a canvass of articulate plastic that has been placed over a drawing of just the y -axis, and that the ten -axis is a skewer stuck through the sail. To flip the graph, plow the skewer 180°. (Pictures here.) Then the new graph, beingness the graph of –h(ten), looks like this:
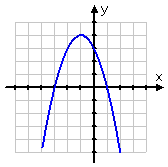
Flipping a function upside-down always works this way: you slap a "minus" on the whole thing. The "flipping upside-down" thing is, slightly more technically, a "mirroring" of the original graph in the x -axis. If yous think of taking a mirror and resting it vertically on the ten -axis, y'all'd see (a portion of) the original graph upside-downwardly in the mirror. When they talk almost "mirroring" or "reflecting" in or about an axis, this is the mental picture they have in listen.
To keep straight what this transformation does, retrieve that f(x) is the exact aforementioned thing as y . So, by putting a "minus" on everything, yous're changing all the positive (in a higher place-centrality) y -values to negative (beneath-axis) y -values, and vice versa. (Whatsoever points on the x -axis stay correct where they are. Information technology's only off-axis points that motility.)
The previous reflection was a reflection in the 10 -axis. This leaves usa with the transformation for doing a reflection in the y -axis.
For this transformation, I'll switch to a cubic part, being g(x) = x three + 10 two – 3x – 1.
Here's the graph of the original function:
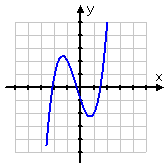
If I put –x in for x in the original function, I go:
g(–ten) = (–x)three + (–x)2 – three(–x) – 1
= –ten 3 + ten 2 – (–threex) – one
= –x 3 + 10 2 + 3x – i
This new role graphs like this:
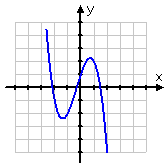
This transformation rotated the original graph around the y -axis. Any points on the y -axis stay on the y -centrality; information technology's the points off the axis that switch sides. This is always true: g(–ten) is the mirror epitome of yard(x); plugging in the "minus" of the argument gives you a graph that is the original reflected in the y -axis.
To keep straight what this transformation does, remember that you're swapping the x -values. Any you'd gotten for x -values on the positive (or right-hand) side of the graph, you're at present getting for x -values on the negative (or left-hand) side of the graph, and vice versa. Since the inputs switched sides, so besides does the graph.
-
Given the graph below of a function f(x), determine which of Graphs A and B represent f(–x) and –f(x).
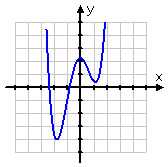
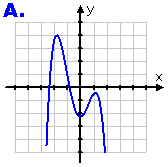
They've given me Graph A:
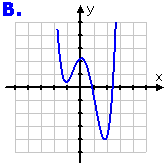
...and Graph B:
Comparing Graphs A and B with the original graph, I can see that Graph A is the upside-downward version of the original graph. It's been reflected across the ten -centrality. This means that information technology's the "minus" of the original function; it's the graph of –f(x).
Graph B has its left and right sides swapped from the original graph; it's been reflected across the y -axis. That ways that this is the "minus" of the function's argument; it'southward the graph of f(–x).
Graph A represents –f(x)
Graph B represents f(–x)
-
Given the function f(x) = ten two + x – iii, find the part statements, in simplified course, for the reflection of the function in each of the x - and y -axes. Label the reflections appropriately.
Well, "appropriately" is a trivial vague; I'll merely be sure the characterization everything very clearly.
I need to observe the simplified functional statements for each of the reflections. One of the reflections involves putting a "minus" on the function; the other involves putting a "minus" on the argument of the function. So I'll practise each of these.
First upwardly, I'll put a "minus" on the argument of the function:
f(–x) = (–x)2 + (–x) – 3
= x 2 – ten – 3
At present for the other reflection:
–f(x) = –(10 2 + x – 3)
= –x two – x + 3
Putting a "minus" on the argument reflects the graph in the y -axis. Putting a "minus" on the whole function reflects the graph in the 10 -axis. So my (conspicuously labelled) answer is:
reflection in the y -centrality:
f(–ten) = x 2 – x – 3
reflection in the x -axis:
–f(x) = –x ii – 10 + three
Many textbooks don't go any further than this. If these are all the rules you need, so write 'em downwards and make certain you've done enough exercise to be able to go along them straight on the next examination:
The function translation / transformation rules:
f(x) + b shifts the role b units upward.
f(x) – b shifts the role b units downward.
f(x + b) shifts the office b units to the left.
f(ten – b) shifts the function b units to the correct.
–f(x) reflects the function in the x -centrality (that is, upside-down).
f(–10) reflects the function in the y -axis (that is, swapping the left and right sides).
Source: https://www.purplemath.com/modules/fcntrans2.htm
0 Response to "How to Know if a Transformationis Telling You to Reflect the X or Y Axis"
Post a Comment